Kürenin Hacmi Nasıl Hesaplanır, Formülü Nedir?

Matematik ve geometri derslerini pek çoğumuz son olarak lise yıllarında görmüş olsak bile aslen bilincinde olmadan günlük hayatta sürekli karşılaşıyoruz. Aslına bakarsan mühendislik benzer biçimde birçok iş alanında geometrik şekiller etken olarak kullanılıyor. Bunlardan bir tanesi de küre. Küre, dışarıdan bakılmış olduğu vakit kolay bir yuvarlak benzer biçimde görünen sadece kusursuz simetriye haiz en mühim geometrik şekillerden bir tanesidir.

Kürenin hacmi, alanı ve benzeri ölçüleri bulmak pek kolay olmadığı için kullanmanız ihtiyaç duyulan hususi bir formülü var. Bu formülü bildikten sonrasında lüzumlu değişkenleri yerlerine yerleştirerek birkaç kolay işlem ile kürenin hacmini bulmanız mümkün. Normal olarak daha karışık işlemlerde kürenin hacmi yalnızca çözümün ilk adımı olabilir. Gelin kürenin hacmi nasıl bulunur sorusuna yakından bakalım ve bu hesaplama işlemi için kullanmanız ihtiyaç duyulan formülü görelim.

Asla bilmeyenler için, küre nedir?

Küre, bakışımlı olarak kusursuz olarak tanımlanan geometrik bir şekildir. Bununla beraber bir yüzey olan küre, üç boyutlu öklit uzayda bulunmaktadır. Günlük hayatta aynı bulunduğunu düşünsek de aslen matematik ve geometride içi dolu ve içi boş küre ayrı şekilde değerlendirilir. İçi dolu küre yuvar olarak adlandırılır. Yuvar üç boyutluyken içi boş küre iki boyutludur. Bir boyutlu küre ise çemberdir. 

Kürenin hacmini hesaplama işlemi için kullanmanız ihtiyaç duyulan hususi formülü:

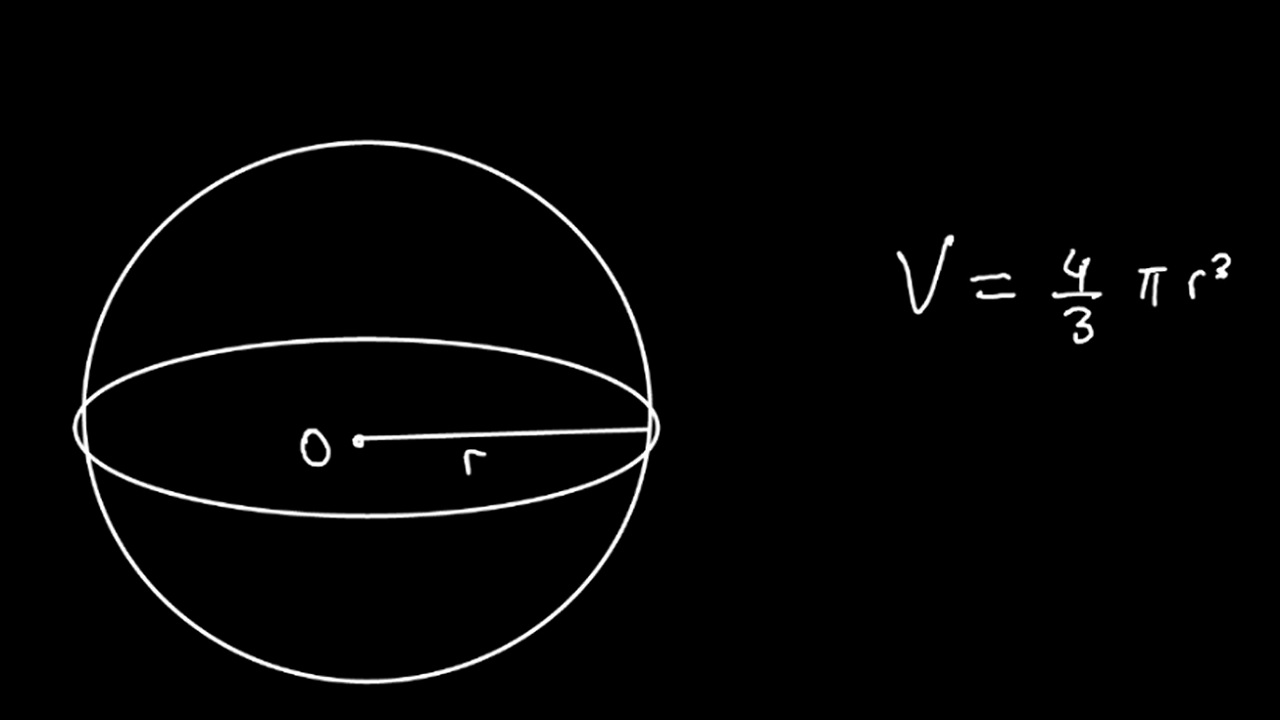
Birazdan örnek üstünden açıklarken detaylarına geçeceğiz fakat ilk olarak kürenin hacmi nasıl ölçülür sorusunun en temel yanıtı olan, bu işlem için kullanmanız ihtiyaç duyulan formülü yazalım. Kürenin hacim hesaplama formülü V = ⁴⁄₃πr³ şeklindedir. Bu formülü derhal bir yere not edin ve kağıt kalem hazırsa derhal örneğimizi incelemeye başlayın.

Kürenin hacmi nasıl hesaplanır? Bir örnek üstünden anlatalım:

• Adım #1: Kürenin hacim hesaplama formülünü bir köşeye yazın.
• Adım #2: Ilk olarak yarıçapı bulun ve formüldeki yerine yazın.
• Adım #3: Yarıçapın küpünü bulun ve formüldeki yerine yazın.
• Adım #4: Küpünü aldığınız yarıçapı formüldeki değerle çarpın.
• Adım #5: Son olarak kazanmış olduğunuz kıymeti pi sayısı ile çarpın.

Adım #1: Kürenin hacim hesaplama formülünü bir köşeye yazın:

Yukarıda bahsettiğimiz benzer biçimde kürenin hacim hesaplama formülü V = ⁴⁄₃πr³ şeklindedir. Eğer usta bir matematikçi değilseniz ve tüm işlemleri aklınızdan yapmayacaksanız ilk olarak bu formülü bir köşeye yazmanız gerekir. Aslına bakarsan sonraki adımları, V = ⁴⁄₃πr³ formülü üstünde uygulamanız gerekecek. Formülde V kürenin hacmini, r ise kürenin yarıçapını ifade etmektedir. 

Adım #2: Ilk olarak yarıçapı bulun ve formüldeki yerine yazın:

Kürenin hacmini hesaplamak için ilk olarak kürenin yarıçapını kısaca r kıymetini bulmak gerekiyor. Bazı sorularda kürenin yarıçapı direkt olarak verilebilir. Bu şekilde bir durum var ise bir sonraki adıma geçebilirsiniz. Eğer kürenin yarıçapı verilmediyse yapmanız ihtiyaç duyulan kürenin çapını ikiye bölmektir. Bu örneğimiz için kürenin yarıçapını 1 santimetre olarak alalım.

Bu aşamada bir ayraç açalım. Bazı sorularda çap ya da yarıçap yerine kürenin yüzey alanı verilir. Bu şekilde bir durumda endişeye kapılmayın ve şu formülü uygulayarak kürenin yarıçapını bulun; r = karekök ( yüzey alanı / 4π )

Adım #3: Yarıçapın küpünü bulun ve formüldeki yerine yazın:

Kürenin yarıçapını bulduğumuza bakılırsa işleme devam etmek için kürenin yarıçapının küpünü almamız gerekiyor. r³ şeklinde gösterilen bu kıymet r x r x r şeklinde bulunabilir. Örneğimizdeki yarıçap 1 olduğundan 1 x 1 x 1 = 1 kısaca r³ = 1. Bu kıymeti formüldeki yerine yazınca şöyleki bir tablo çıkıyor; V = ⁴⁄₃π x 1 

Bu örnekte kolay anlaşılması için kürenin yarıçapını 1 olarak vermemiz kafa karıştırıcı olmasın. Kürenin yarıçapının 2 olduğu durumda 2 x 2 x 2 = 8 kısaca r³ = 8 şeklinde bir netice çıkar. Bazı büyük sayılarda netice da büyük olabilir sadece daima santimetre cinsinden yazmayı dikkatsizlik etmeyin. 

Adım #4: Küpünü aldığınız yarıçapı formüldeki değerle çarpın:

Kürenin yarıçapının küp kıymetini 1 olarak bulduktan sonrasında formüldeki yerine yazınca V = ⁴⁄₃π x 1 şeklinde bir işleme dönüştü. Bu aşamada yapmanız ihtiyaç duyulan ilk işlem r³ kısaca 1 ile 4/3 kıymetini çarpmaktır. 4/3 x 1 = 4/3. Formüldeki yerine koyduğumuz vakit karşımıza V = ⁴⁄₃π şeklinde bir tablo çıkıyor. 

Adım #5: Son olarak kazanmış olduğunuz kıymeti pi sayısı ile çarpın:

Kürenin yarıçapını bulduk, küpünü hesapladık ve formülde olduğu benzer biçimde 4/3 kıymeti ile çarptık. Şimdi sıra geldi V = ⁴⁄₃π formülde olduğu benzer biçimde son adım olan pi sayısı ile çarpmaya. Bu tür işlemlerde pi sayısı, aksi söylenmediği sürece 3,14 olarak formüle dahil edilir. Kısaca V = ( 3,14 ) x 4/3 bu da V = 4,19 oluyor. Tüm bu işlemleri kübik birimler olarak belirlediğimiz için kürenin hacmi kısaca V = 4,19 cm3

Kürenin hacmini hesaplarken dikkat etmeniz gerekenler:

• Formülün üstünde işlem yaptığınız tüm birimlerin aynı olduğundan güvenli olun. Kısaca tüm sayıları metre ya da santimetre cinsinden kullanın.
• Küre öklit uzayda bulunan bir biçim olduğundan tüm birimler m³ şeklinde kübik olmalı.
• Eğer işlemde sizden küre hacminin yarısı ya da çeyreği isteniyorsa gene de ilk olarak tüm hacmi bulun ve sonrasında bunu değerin yarısı için ½, çeyreği için ¼ ile çarpın.

Küre işlemlerinde kullanabileceğiniz öteki formüllerden bazıları:

• Kürenin projeksiyon alanı: APF = 4/3πr²
• Kürenin parça hacmi: VKS = h²π / 3 ( 3r – h )
• Kürenin atalet momenti: J = 2 / 5 x mr²
• Kürenin yüzey alanı: A = 4πr² = d²π

Matematik ve geometride karşımıza çıkan kusursuz simetriye haiz kürenin hacmi nasıl hesaplanır sorusunu yanıtlayarak hesaplama işlemi için kullanabileceğiniz formülü paylaştık. Normal olarak küre son aşama karmaşık bir mevzu sadece bu yazımızda asla bilmeyenler için genel bir bilgilendirme yapmayı hedefledik.